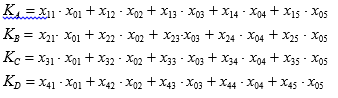Применение анализа иерархий для решения задач выбора оптимальной альтернативы

Метод анализа иерархий (МАИ) – математический инструмент системного подхода к сложным проблемам принятия решений. Этот метод разработан американским ученым Томасом Л Саати в 1970 году, с тех пор он активно развивается и широко используется на практике.

3.1. Описание МАИ

В соответствии с МАИ, для реализации метода необходимо осуществить следующие

этапы.

1. Очертить проблему и определить, что необходимо узнать.
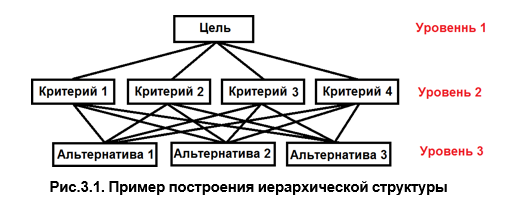
2. Построить иерархическую структуру. Иерархическая структура – это представление проблемы в виде перевернутого дерева, где каждый элемент, за исключением самого верхнего, зависит от одного или более выше расположенных элементов.
Вершиной иерархии является Цель; элементы промежуточных уровней соответствуют Критериям, которые связывают цель с Альтернативами. Каждая Альтернатива – это дочерний элемент каждого из включающих ее Критериев.

Пример иерархической структуры, представлен на рис.3.1.






3. Определить значимости критериев. Эту операцию под руководством лица, принимающего решение (ЛПР), осуществляет бригада экспертов, использующих методы групповых парных сравнений. Результаты сравнений переводятся в числа по шкале относительной важности Т. Саати (табл.3.2).
4. Построить множество матриц парных сравнений для каждого из нижних уровней – по одной матрице для каждого элемента, примыкающего сверху уровня.
5. Использовать иерархический синтез для получения наилучшего варианта (п.3).

3.1. Экспертное оценивание

В общем случае экспертное оценивание можно определить так: задано некоторое множество А={Аk} (k=1,2, …, n), альтернатив, которые нужно сравнить по


некоторому множеству критериев, с целью определения относительных коэффициентов значимости wk/

Парные сравнения приводят к матричной форме - квадратной матрице парных сравнений (табл.3.1).

	А1	А2	…	Аn
А1	w1 w1	w1 w2	…	w1 wn
А2	w2 w1	w2 w2	…	w2 wn
…	…	…	…	…
Аn	wn w1	wn w2	…	wn wn

В силу разнородности критериев оценки экспертами проводятся по шкале относительной важности (табл.3.2).

По соглашению сравнивается относительная важность левых элементов матрицы относительно диагонали с элементами наверху. Поэтому если элемент слева от диагонали матрицы важнее, чем элемент сверху диагонали, то в клетку заносится положительное число (от 1 до 9) в противном случае – обратное число (дробь).

Например, если элемент А воспринимается как «слегка более важный» (3 по шкале) относительно В , то считаем, что элемент В «слегка менее важен» (1/3 по шкале).

Относительная важность любого элемента сравниваемого с самим собой равна 1, поэтому диагональ матрицы содержит единицы.

Интенсивность относительной важности	Определения	Объяснения
1	Равная важность	Равный вклад двух видов деятельности в цель
3	Умеренное превосходство одного над другим	Опыт и суждения дают легкое превосходство одному виду деятельности над другим
5	Существенное или сильное превосходство	Опыт и суждения дают сильное превосходство одному виду деятельности над другим
7	Значительное превосходство	Одному виду деятельности дают настолько сильное превосходство, что оно становится практически значимым
9	Очень сильное превосходство	Очевидность. Превосходство одного вида деятельности над другим подтверждается наиболее сильно
2, 4, 6, 8	Промежуточные решения между двумя соседними суждениями	Применяются в компромиссном случае

3.4. Синтез приоритетов

Из группы парных сравнений формируется набор локальных приоритетов, которые выражают относительное влияние множества элементов на элемент, примыкающего сверху уровня.

Одним из способов определения приоритетов является вычисление геометрического среднего. Это можно сделать, перемножая элементы в каждой строке и извлекая корень n - й степени, где n – число элементов. Последовательность расчета составляющих вектора приоритетов представлена в табл. 3.3.





Здесь сумма = a1 + a2 + L + an .

3.4. Пример применения МАИ

Для уборки зерновых культур необходимо приобрести зерноуборочный комбайн. На рынке имеются машины четырех фирм: А, В, C, D одинакового целевого назначения. Какой зернокомбайн выбрать в соответствии с потребностями покупателя?

3.4.1. Представим задачу в иерархической форме

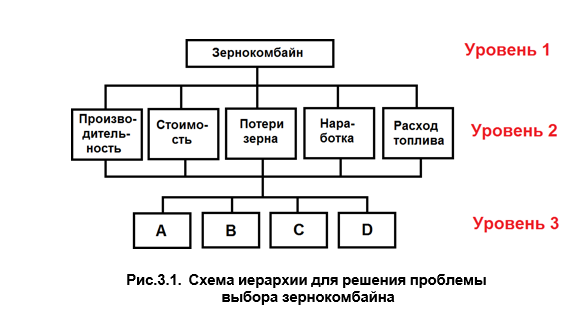
На первом (высшем) уровне находится общая цель «Зернокомбайн» (рис.3.1). На втором уровне втором уровне находятся четыре показателя (критерия), уточняющие цель. На третьем (нижнем) уровне находятся машины кандидаты (варианты решения), которые должны быть оценены по отношению к критериям второго уровня.

3.4.1. Составим матрицы попарных сравнений

4.1.1. Матрица попарных сравнений для уровня 2

Установим приоритеты критериев и оценим каждую из альтернатив по критериям, выявим тем самым самую предпочтительную из них. Для количественного определения сравнительной важности факторов и проблемной ситуации составим матрицу попарных сравнений (табл.3.4).

Общее удовлетворение комбайном	Пр.	Пз.	Нар.	Рт.	Ст.
Производительность (Пр)	1	5	4	5	3
Потери зерна (Пз)	1/5	1	1/2	2	1/2
Наработка (Нар)	1/4	2	1	2	1/4
Расход топлива (Рт)	1/5	1/2	1/2	1	1/2
Стоимость (Ст)	1/3	2	4	2	1

3.4.1.1. Матрицы попарных сравнений для уровня 3

В данном примере нужно составить пять матриц для третьего уровня по отношению к критериям второго уровня. Эти матрицы строятся по объективным показателям (табл.3.10), использующимся для сравнения комбайнов и взятых из протоколов испытаний, научной литературы, рекламных проспектов.

Производительность	A	B	C	D
A	1	13/21	13/12	13/18
B	21/13	1	21/12	21/18
C	12/13	12/21	1	12/18
D	18/13	18/21	18/12	1

Потери зерна	A	B	C	D
A	1	3/2	2/2	3/2
B	2/3	1	2/3	3/3
C	2/2	3/2	1	3/2
D	2/3	3/3	2/3	1

Наработка	A	B	C	D
A	1	160/119	160/120	160/130
B	119/160	1	119/120	119/130
C	120/160	120/119	1	120/130
D	130/160	130/119	130/120	1

Расход топлива	A	B	C	D
A	1	30/29	24/29	27/29
B	29/30	1	24/30	27/30
C	29/24	30/24	1	27/24
D	29/27	30/27	24/27	1

Стоимость	A	B	C	D
A	1	1100/900	1050/900	1200/900
B	900/1100	1	1500/1100	1200/1050
C	900/1050	1100/1050	1	1200/1050
D	900/1200	1050/1200	1050/1200	1

Показатель	A	B	C	D
Производительность, т/ч	13	21	12	18
Потери зерна, %	2	3	3	3
Наработка, час.	160	119	120	130
Расход топлива, л/ч	29	30	24	27
Стоимость, тыс. руб.	900	1100	1050	1200

3.4. Синтез приоритетов

Для данных, приведенных в табл.3.4, значение вектора приоритетов будут следующими (табл.3.11)

Общее удовлетворение комбайном	Вектор приоритетов
Производительность	0,491
Потери зерна	0,099
Наработка	0,104
Расход топлива	0,086
Стоимость	0,220

В табл.3.12 представлены векторы приоритетов для третьего уровня иерархии, иллюстрирующие сравнительную желательность вариантов марок комбайнов по отношению к критериям второго уровня

Вариант решения	Производи- тельность	Потери зерна	Наработка	Расход топлива	Стоимость
1	2	3	4	5	6
А	0,203	0,3	0,235	0,302	0,292
B	0,328	0,2	0,228	0,225	0,239
C	0,188	0,3	0,284	0,227	0,250
D	0,281	0,2	0,253	0,246	0,291

Вычислим глобальные приоритеты. Для этого локальные приоритеты уровня 3 (табл.3.12) перемножаются на приоритеты соответствующих критериев уровня 2 (табл.3.11) и суммируются.



Вариант решения А:

КA=0,203 х 0,491+0,3х0,099+0,235х0,104+0,302х0,086+0,292х0,220=0,246

Вариант решения B:

КB=0,328 х 0,491+0,2х0,099+0,228х0,104+0,225х0,086+0,239х0,220=0,210

Вариант решения C:

КC=0,188 х 0,491+0,3х0,099+0,284х0,104+0,227х0,086+0,250х0,220=0,273

Вариант решения D:

КD=0,281 х 0,491+0,2х0,099+0,253х0,104+0,246х0,086+0,291х0,220=0,233



Вывод. На основе проведенных вычислений вариант C получает наивысший вес и, следовательно, является наиболее оптимальным.

3.4. Формализация алгоритма МАИ

Рассмотрим применение алгоритма на рассмотренном выше примере п.2.

3.4.1. Исходные данные:

Задание экспертных оценок для формирования табл.3.4



a21=1/5 a31=1/4 a32=2

a41=1/5 a42=1/2 a43=1/2 a51=1/3 a52=2 a53=4 a54=2

Задание сравнительных характеристик комбайнов (табл.3.10)

b11= 13	b11= 21	b11= 12	b11= 18
b11= 2	b11= 3	b11= 3	b11= 3
b11= 160	b11= 119	b11= 120	b11= 130
b11= 29	b11= 30	b11= 24	b11= 27
b11=900	b11=1100	b11=1050	b11=1200

3.4.1. Алгоритмы вычислений.

4.1.1. Расчет матрицы попарных сравнений, построенной на основе экспертных оценок (табл.3.4).

a11=1	a12=1/ a21	a13=1/ a31	a14=1/ a41	a15=1/ a51
a21	a22=1	a23=1/ a32	a24=1/ a42	a25=1/ a52
a31	a32	a33=1	a34=1/ a43	a35=1/ a53
a41	a42	a43	a44=1	a45=1/ a54
a51	a52	a53	a54	a55=1

Расчет среднего геометрического (табл.1.3)





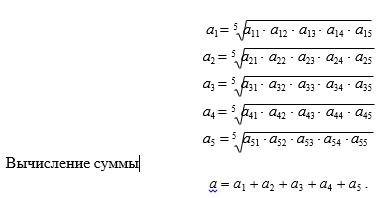
Нормализация вектора приоритетов для второго уровня иерархий, вычисленного на основе экспертных оценок (результаты расчета табл.3.11)

Общее удовлетворение комбайном	Вектор приоритетов
Производительность	x01 = a1 / a
Потери зерна	x02 = a2 / a
Наработка	x03 = a3 / a
Расход топлива	x04 = a4 / a
Стоимость	x05 = a5 / a

3.4.1.1. Расчет характеристик уровня 3

Организовать цикл k = 1, 2,L, 5 . Для каждого значения k вычислить:



a) матрицу парных сравнений для уровня 2

c11=1	c12=1/ c21	c13=1/ c31	c14=1/ c41
c21= bk1/ bk2	c22=1	c23=1/ c32	c24=1/ c42
c31= bk1/ bk3	c32= bk2/ bk3	c33=1	c34=1/ c43
c41= bk1/ bk4	c42= bk2/ bk4	c43= bk3/ bk4	c44=1

b) компоненты вектора приоритетов как среднее геометрическое по строке (табл.3.3)





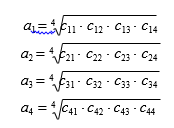
c) сумму вычисленных значений среднего геометрического
a = a1 + a2 + a3 + a4 .


d) координаты нормализованного вектора приоритетов

xk1 = a1 / a xk 2 = a2 / a xk 3 = a3 / a xk 4 = a4 / a .


Замечание. Пункты a, b, c, d вычисляются для каждого значения k.

При k=1 формируется матрица парных сравнений вариантов с точки зрения производительности (табл.3.5). Результаты расчета – координаты вектора приоритетов (второй столбец табл.3.12).

При k=2 формируется матрица парных сравнений вариантов с точки зрения потерь зерна (табл.3.6). Результаты расчета – третий столбец табл.3.12.

При k=3 формируется матрица парных сравнений вариантов с точки зрения наработки (табл.3.7). Результаты расчета – четвертый столбец табл.3.12.

При k=4 формируется матрица парных сравнений вариантов с точки зрения расхода топлива (табл.3.8). Результаты расчета – пятый столбец табл.3.12.

При k=5 формируется матрица парных сравнений вариантов с точки зрения стоимости (табл.3.9). Результаты расчета – шестой столбец табл.3.12.

В результате получаем матрицу векторов приоритетов для третьего уровня иерархий (табл.3.12)

Вариант решения	Производи- тельность	Потери зерна	Наработка	Расход топлива	Стоимость
1	2	3	4	5	6
А	x11	x12	x13	x14	x15
B	x21	x22	x23	x24	x25
C	x31	x32	x33	x34	x35
D	x41	x42	x43	x44	x45

e) вычислить глобальные приоритеты