История динамического программирования
Динамическое программирование возникло и сформировалось в 1950–1953 гг. благодаря работам Ричарда Беллмана и его сотрудников. Беллман (Bellman) Ричард Эрнест (1920-84) – американский математик. Первыми задачами, решаемыми с помощью динамического программирования были задачи управления запасами.Задача динамического программирования
Задачи динамического программирования укладываются в следующую схему:I. Имеется набор способов действий – допустимых управлений.
II. Имеется целевая функция («прибыль», «убыток») S = S(u), где u пробегает допустимые управления.
Требуется выбрать управление, которому отвечает оптимальное значение целевой функции.
Формализация задачи динамического программирования
Динамическая система (ДС) – такой объект, который может развиваться.Квазидинамическая система – система, которую можно привести к динамической.
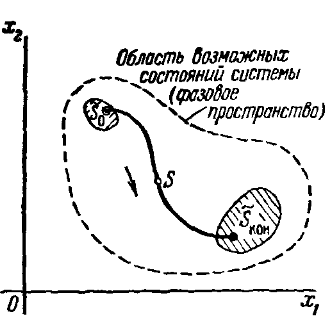
Пространство состояний (фазовое пространство) динамической системы – множество всех возможных состояний динамической системы.
ДС с дискретным временем – ДС, состояние которой меняется в дискретные моменты времени, например, t0, t1,t2,..,tn.
Траектория – набор состояний, через которые проходит ДС от начального к конечному состоянию.
Управляемая ДС – ДС, траекторию которой можно менять с помощью управляющих импульсов Uk.
Функционирование динамической модели
- В начальный момент времени t0 система находится в фиксированном состоянии x0.
- Переход xk-1 ® xk от состояния в момент tk-1 к состоянию в момент tk (от t0 к t1 от t1 к t2 и т.д.) осуществляется под воздействие управляющих сигналов uk , т.е. xk =j(xk-1 , uk). Набор состояний x0, x1 ,…, xn – траектория ДС. Причем, начало всех траекторий одинаковое - x0.

Общая задача динамического программирования
Пусть имеется управляемая динамическая система оценивается каким-либо показателем, например, суммарным доходом S=S(u1,u2,..,un). Суммарный доход равен сумме доходов на каждом шагеS=f1+f2+…+fn. (1)
fk – доход на k-ом шаге, который зависит от состояния ДС в начале k-го шага и выбранного управления uk:
fk = fk(xk-1 , uk) (2)
Подставляя (1) в (2) получим:
Такая функция называется аддитивной целевой функцией.
Для анализа имеется управляемая динамическая система, для которой выделено n шагов, а на каждом шаге выделены все возможные состояния (xk), через которые проходит система, а также выделено начальное состояние x0, а на каждом шаге заданы возможные управляющие воздействия (uk). Также имеется аддитивная функция.
Задача ДП состоит в том, чтобы найти такую последовательность управляющих воздействий во время функционирования ДС (u1,u2,…,un), чтобы аддитивная функция S достигала максимума или минимума. Траектория, на которой достигается max или min целевой функции, называется оптимальной траекторией. Задачей ДП является отыскание оптимальной траектории.
Метод решения задачи динамического программирования
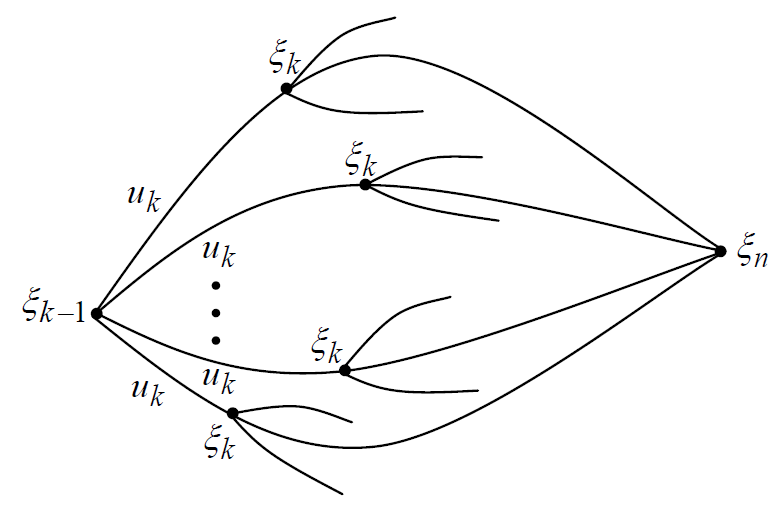
Предположим, что к на- чалу k-го шага система оказалась в состоянии xk-1. Оставшийся путь до конца система может проходить по различным траекториям в зависимости от выбора последующих управлений. Каждой траектории отвечает свой суммарный доход, т.е. доход на участке Обозначим этот доход через Sk.
Sk=fk+fk+1+…+fn
S*k(xk-1) – условный максимальный доход – максимальный суммарный доход, начиная с k-го шага и до конца, т.е. на участке [k-1,n]. Тогда основную задачу ДП можно формализовать в виде:
И требуется найти условное оптимальное управление на k-м шаге u*k(xk-1).
Задачи ДП решаются в два этапа:
- движение от конца к началу
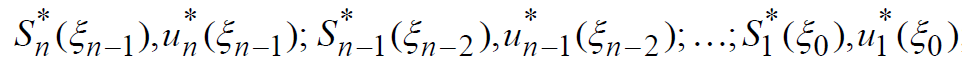
для всех возможных на соответствующих шагах состояний с использованием на каждом шаге, начиная с n-1-го, формулы для
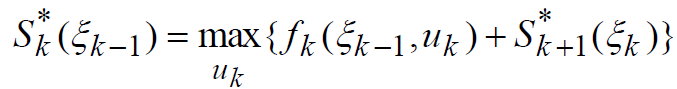
Задачи ДП решаются в два этапа:
- движение от конца к началу
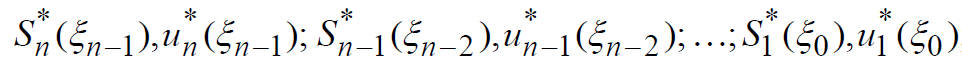
для всех возможных на соответствующих шагах состояний с использованием на каждом шаге, начиная с n-1-го, формулы для
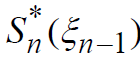
2. движение от начала к концу
Двигаясь от начала, существенно используя закрепленность начального состояния, строим безусловную оптимальную траекторию.



